Generalization of Quantum Mechanical Wave Equation in Spherical Coordinate Using Great Metric Tensors and a Variable Gravitational Scalar Potential
Published: 2020-07-30
Page: 139-147
Issue: 2020 - Volume 2 [Issue 1]
A. U. Maisalatee *
Department of Physics, Nasarawa State University, Keffi, P.M.B. 1022, Nigeria.
W. L. Lumbi
Department of Physics, Nasarawa State University, Keffi, P.M.B. 1022, Nigeria.
I. I. Ewa
Department of Physics, Nasarawa State University, Keffi, P.M.B. 1022, Nigeria.
M. Mohammed
Department of Physics, Nasarawa State University, Keffi, P.M.B. 1022, Nigeria.
Y. K. Kaika
Department of Physics, Nasarawa State University, Keffi, P.M.B. 1022, Nigeria.
*Author to whom correspondence should be addressed.
Abstract
In this research work, the Riemannian Laplacian operator for a spherical system which varies with time, radial distance and time was obtained using the great metric tensors and a varying gravitational scalar potential. Furthermore the obtained Laplacian operator was used to obtain the generalized quantum mechanical wave equation for particles within this field. The Laplacian operator obtained in this work reduces to the well known Laplacian operator in the limit of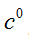 
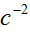
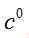
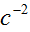
, and it contained post Euclid or pure Riemannian correction terms of all orders of 
. Also the generalized quantum mechanical wave equation obtained, in the limit of 
reduces to the well known Schrodinger mechanical wave equation, and in the limit of 
contained additional correction terms not found in the well known Schrodinger wave equation. Hence the results in this work satisfy the Principle of Equivalence in Physics.
Keywords: Riemannian, minkowski, laplacian, schrodinger, scalar potential
How to Cite
Downloads
References
El Naschie MS. A review of E-infinity theory and the mass spectrum of high energy particle physics. Chaos, Solitons and Fractals. 2004;19;209-236.
Marek-Crnjac L. Quantum Gravity in Cantorian Space-Time, Quantum Gravity, Dr. Rodrigo Sobreiro (Ed.). 2012;87-88.
ISBN: 978-953-51-0089-8.
Ord G. Fractal space-time. J. Phys. A: Math. Gen. 1983;16;18-69.
Ord G. Entwined paths, difference equations and the Dirac equation. Physics Review A. 2003;67:0121XX3.
Daniel R. Bes. Quantum mechanics, A modern and concise introductory course, third edition, Springer, Heidelberg Dordrecht London, New York, p.vii; 2012.
Cruz Y, Cruz S. Negro J, Nieto LM. Classical and quantum position-dependent mass harmonic oscillators, Physics Letters A. 2007;369:400-406.
El Naschie MS. On the Universal behavior and statistical mechanics of multidimen-sional triadic cantor Sets. SAMS. 1993;11: 217-225.
Prigogine I, Rössler O, El Naschie MS. Quantum mechanics, diffusion and chaotic fractals. Pergamon; 1995.
ISBN: 0 08 04227 3.
El Naschie MS. Quantum Collapse of Wave Interference Pattern in the Two-Slit Experiment: A set Theoretical Resolution. Nonlinear Science Letters A. 2001;2(1): 1-9.
He JH. Quantum Golden Mean Entanglement Test as the Signature of the Fractality of Micro Space-time. Nonlinear Science Letters B. 2011;1(2):45-50.
Mauldin RD, Williams SC. Random recursive construction. Trans. Am. Math. Soc. 1986;295:325-346,
El Naschie MS. Superstrings, knots and non-commutative geometry in E- infinity space. Int. J. Theoret. Phys. 1998;37(12): 212-234
El Naschie MS. Elementary prerequisites for E-infinity (Recommended background readings in nonlinear dynamics, geometry and topology). Chaos, Solitons and Fractals. 2006;30;579-605.
El Naschie MS. The concept of E-Infinity: An elementary introduction to the Cantorian–fractal theory of quantum physics. Chaos, Solitons and Fractals. 2004;22:495-511.
Marek Crnjac L. A Feynman path like-integral method for deriving the four dimensionality of space-time from first principle. Chaos, Solitons and Fractals. 2009;41:2471-2473.
El Naschie MS. Quantum gravity from descriptive set theory. Chaos, Solitons and Fractals. 2004;19: 1339-1344.
Lumbi WL, Ewa II, Tsaku N. Einstein’s equations of motion for test particles exterior to spherical distributions of mass whose tensor field varies with time, radial distance and polar angle. Archives of Applied Science Research Library. 2014; 6(5):36-41.
Howusu SXK. The Metric Tensors for Gravitational Fields and The Mathematical Principles of Riemann Theoretical Physics, Jos University Press Ltd. 2009;19-110.
Howusu SXK. The 210 Astrophysical Solutions Plus 210 Cosmological Solutions of Einstein’s Geometrical Gravitational Field Equations. Jos University Press, Jos. 2007;6-29.
Norse T. Foundations of Quantum Mechanics, Undergraduate Lecture note. Springer, Heidelberg Dordrecht London, New York. 2017;33-36.
Maisalatee AU, Chifu EN, Lumbi WL, Sarki MU, Mohammed M. Solution of Einstein’s field equation exterior to a spherical mass with varying potential. Dutse Journal of Pure and Applied Sciences (DUJOPAS). 2020;6(2):294-301
Spiegel MR. Vector Analysis and Introduction to Tensor Analysis. McGraw Hill, New York. 1974;166-217.
Ewa II, Howusu SXK, Lumbi WL. Quantum Energy of a Particle in a Finite Potential Well based upon the Golden Metric Tensor. Physical Science International Journal. 2019;22(3):1-9.